In this post we will show the mathematical similarities and highlight the common factors in three different geostatistical methods: Kriging, implicit modelling and ML. No need to be (very) afraid when quickly scanning the document for all the equations. We have kept them as simple as possible to focus on similarities and a basic understand of the various techniques. However, a basic understanding of Matrices and Vectors is essential. We have unified the variables and terms used in different books and articles to make it easier to understand the different methods.

The purists (some mathematicians and geostatisticians) will likely get goosebumps when reading this. To those, we provide references to books and articles where they can find all the lovely details 😊.

For the exceptional geologist out there, that finds all this mathematical background as intriguing as we do, some of the references at the end I listed as recommended reading as they transformed our understanding of this topic. OK, let’s get going.

A short recap

In our previous posts we introduced the general concept of weighted averaging as a fundamental idea for interpolation and estimation. We demonstrated how a simple average can be calculated and extended it to weighted averages. From there we  introduced more advanced interpolation techniques that provide different ways to calculate the weighting factors used for estimation, such as Kriging and RBFs

In general, an interpolation can be summarized as the weighted sum of known sample data:

\[e\verb|(|s_0\verb|)|= \sum_{i=1}^{n} \omega_i z\verb|(|s_i\verb|)|\]

Here, $s_0$ is the location at an unknown point (where we have not sampled), n is the number of known points (samples), z(s_i) are the measured values at the sample locations, (s), and ω_i is the weighting factor for a known sample. So, again, it is just a sum of weights * sample values.

It’s all about the weights

Different interpolation techniques (also referred to as regression), like Inverse Distance Weighting (IDW), Kriging, RBFs and Machine Learning (ML) each have their own method to establish those weights. Each method in turn has a number of variants, but all of them provide ways to establish the weighting factors for the sample points to produce an estimate.

Below we will briefly mention each of the methods of establishing those weights, before showing some of the similarities between the methods.

Short note: in geology we primarily deal with spatial data and therefore interpolation is typically done in 3D. All of the below is written with this in mind, but most of what we wrote is applicable in other dimensions, ie. other types of data, as well.

Inverse distance weighting (IDW)

As already discussed, in IDW the weights are estimated in one of the simplest ways. Each weight depends on the distance from the sample points to the unknown location:

\[\frac{1}{d^p}\]

The power p determines how quickly the influence of points further away diminishes. Typically, p = 2 for 2D data and p = 3 for 3D data.

To normalize the final estimate, each weight is divided by the sum of all the individual weights. This makes sure the weights add up to 1.

It is a simple and effective method at small distances, but has known issues that are reported in various articles, books etc. E.g., C.D. Lloyd: “Local models for spatial analysis”. So, most people switch to a more advanced method, commonly Kriging.

Kriging

This method also hardly needs any introduction. Many books and articles have covered Kriging and its many variants in fine detail [Chiles and Delfiner, Local models for spatial Analysis, Jackie Coombes]. Here we will merely focus on Simple and Ordinary Kriging following the same approach as in Local Models. Not because they are always the best Kriging methods, but due to their mathematical similarity with other methods described later.

In Kriging the weights are established as follows:

\[\omega = K^{-1} k\verb|(|s_0 \verb|)|\]

We denote here $\omega$ as the Vector containing all the weights, $\omega_i$, for i = 1..n. K is the Covariance matrix containing all the covariances between all samples in Simple Kriging, or semivariances for Ordinary Kriging. k(s₀) is a Vector with covariances or semivariances respectively. It contains the values between the unknown location s₀ and all known samples.

The Matrix K (covariance matrix) and Vector k (covariance vector to unknown location) will play a very important role and we’ll go into more detail later. Just remember that for now.

As said, K is a matrix and because it contains the covariances between each sample and every other sample, it can grow extremely large. E.g. for 100 points, the K matrix contains 100*100 = 10,000 values.

Calculating the inverse of K becomes extremely slow when we have more than few 10’s of thousands of samples and is partly why different methods have been developed. But for now, we just want to explain the basic formulas.

With the above weights vector, we rewrite our estimate a little to a Vector notation:

\[z \verb|(|s_0 \verb|)| = \omega z \verb|(|s \verb|)|^T\]

Kriging estimate

So, the estimate becomes a Vector * Vector multiplication of weights * sample values. In other words, it is a dot product of the 2 vectors: the weights Vector and the sample values Vector.

Due to the large size of the Matrix K for large point sets and the relatively limited influence points far away have on local points, Kriging is often implemented as a moving average. A local search radius is used to select only the nearest points and those are used to calculate the weights as above. The downside of course is that the weights need to be estimated every time, a time-consuming process.

Paradigm shift: Dual Kriging and RBFs

To improve the speed of Kriging estimation there is a faster method, called Dual Kriging. Here instead of our weighted sum we first fit a set of weights to our known values. To demonstrate, let’s rewrite the above again to show how. Using the definition of Kriging weights for our estimation we get:

\[e \verb|(| s_0 \verb|)| = K^{-1} k_0 z \verb|(|s \verb|)|\]

However, we can also turn this around to estimate the weights like so:

\[ \omega = K^{-1} z \verb|(| s \verb|)| \]

The estimate is then calculated as:

\[ e \verb|(| s_0 \verb|)| = \omega k_0\]

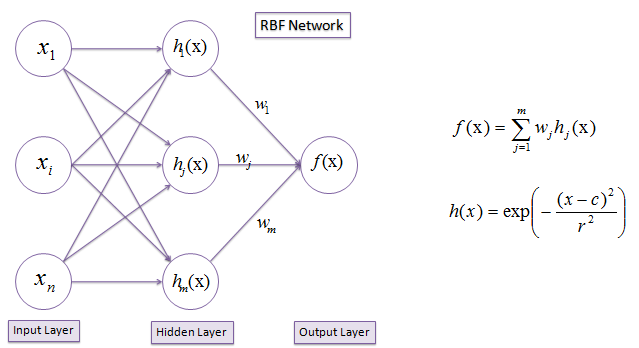
This is called the Dual Kriging method (See Fast Multidimensional Interpolations, Horowitz et. al 1996) and can be shown to be computationally faster. Don’t ask me, but some clever mathematicians. But it makes sense once you think about it: you calculate the weights only one time for all the know samples (and its covariance matrix). After that you can estimate at any point just using the local covariances k₀. There is no need to compute a new K every time.

As it turns out this is nearly identical to creating estimates with RBFs typically used for implicit modelling nowadays. Officially the RBF is calculated like this:

\[e \verb|(| s_0 \verb|)| = \omega k_0 + P \verb|(| s \verb|)|\]

The term P(s) is some polynomial depending on the sample points. If it is 0, it becomes exactly the Dual Kriging solution. And when P(s) is not 0, it can be regarded as an estimated trend similar to that in universal Kriging, according to Fast Multidimensional Interpolations… The last are not my words…

Now, onto ML

Machine Learning (ML) approach

In ML the two most common techniques for many AI systems depend on some neural network (NN) or a support vector machine (SVM). We’ll handle both but will start with SVMs due to its similarity to RBFs.

SVMs

An estimate calculated using an SVM is defined as follows:

\[e \verb|(| s_0 \verb|)| = \omega k_0 + b\]

This should look very familiar by now. Again, we have a set of weights again multiplied by the covariances. In addition, there is a term b, which is called the bias and is just a constant. If b = 0 it is again similar to Dual Kriging.

NNs

In neural networks, we again can create prediction in a similar fashion. Let’s take a very simple network:

I chose this image as it is using 3 inputs, like our XY Z, to produce a prediction, here called f(x).

Notice how the prediction is calculated: sum of weights * local covariances. Yes, it’s the same as before in Dual Kriging:

\[ e \verb|(| s_0 \verb|)| = \omega k_0\]

But here z(s₀) is called f(x), and h(x) are our local covariances k₀. I also chose this type of network as it is called an RBF network, thus highlighting its use of a Radial Basis Function in the hidden layer, which we’ll come back to in more detail in the next section.

Partial summary

Before moving on to more intricate details for establishing the weights, a short summary. As we have demonstrated the estimation on a resource using geostatistics generally comes down to establishing the weights and multiplying them with the known sample values. However, using the known sample values (and locations of course) we can turn the calculations around to obtain a global fitted implicit function in the form of Dual Kriging, RBF or ML. This means that main difference in the methods is in how those weights are calculated. That is what we will focus on in our next post.